Главное меню
Присоединяйтесь
В сопротивлении материалов при растяжении или сжатии под действием силы Р рассматривают нормальные напряжения σ, распределенные равномерно по поперечному сечению стержня, соответственно:

где S ‒ площадь поперечного сечения стержня, м2.
Правило знаков в сопромате для нормальных напряжений аналогично правилу для продольных сил в строительной механике: если сила растягивает стержень, то "+", если сжимает "‒".
Под действием силы Р стержень длиной l удлиняется на величину Δl, которая называется абсолютным удлинением. При этом выделяют относительную продольную деформацию, определяемую по формуле:
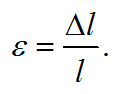
Для упругих материалов в сопромате действует Закон Гука, представляющий собой зависимость между нормальным напряжением σ и относительной деформацией ε:
![]()
где Е - модуль продольной упругости (модуль Юнга), Па.
Из закона Гука можно определить абсолютное удлинение стержня:

Абсолютное удлинение стержня под действием только собственного веса определяется по формуле:

где γ ‒ удельный вес материала стержня, Н/м3.
Проверочный расчет на прочность стальных конструкций в сопротивлении материалов при растяжении-сжатии выполняется по зависимости:
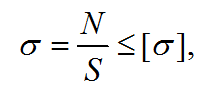
где [σ] ‒ допускаемое напряжение, Па.
Ниже приведен пример решения задачи по данной теме.
Задача
Исходные данные: Р=10 кН; S=0,3 м2; Е=2,1·105 МПа.
Необходимо построить эпюры нормальных сил и напряжений. Определить перемещение нижнего конца стержня (бруса), представленного на рисунке 1, а. Все размеры на рисунке 1 даны в метрах.
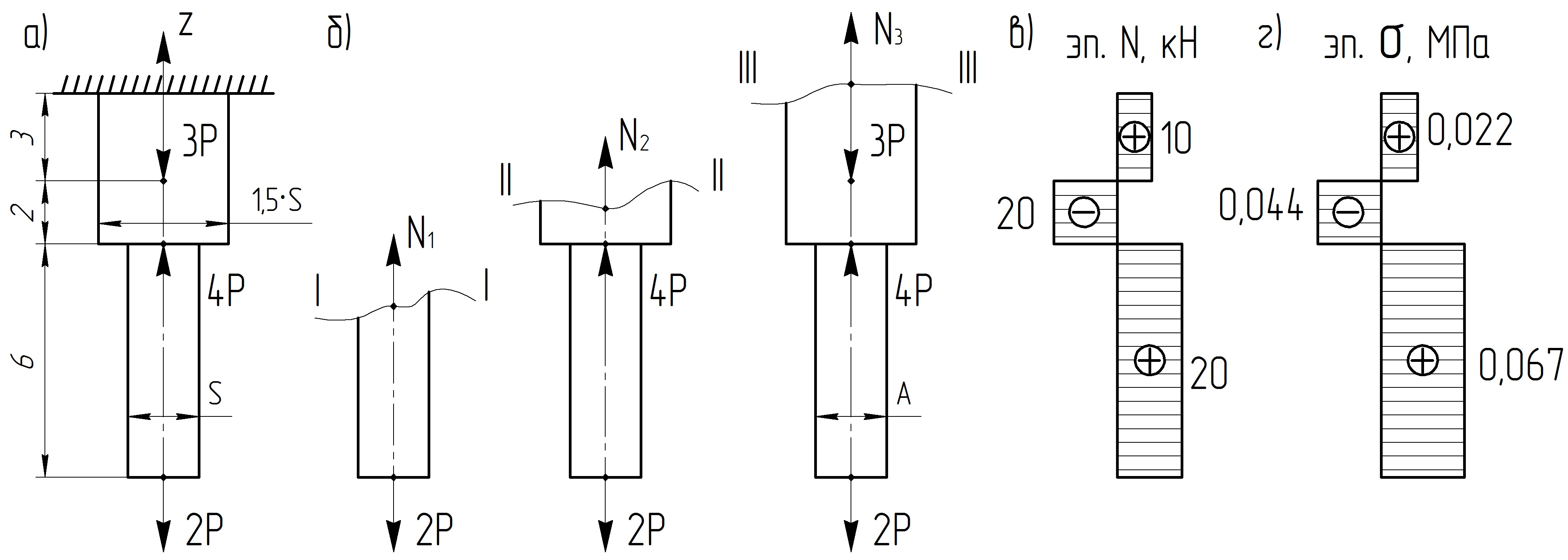
Рисунок 1 ‒ Схема стержня и эпюры напряжений
Вначале стержень разбивается на участки, границами которых являются точки приложения сосредоточенной силы и изменения площади поперечного сечения.
Для каждого участка составляется уравнение равновесия (рисунок 1, б):
Участок 1: 0 ≤ z ≤ 6:
![]()
Участок 2: 6 ≤ z ≤ 8:
![]()
Участок 3: 8 ≤ z ≤ 11:
![]()
Строим эпюру нормальных сил (рисунок 1, в).
Для каждого рассмотренного участка определяем нормальные напряжения:
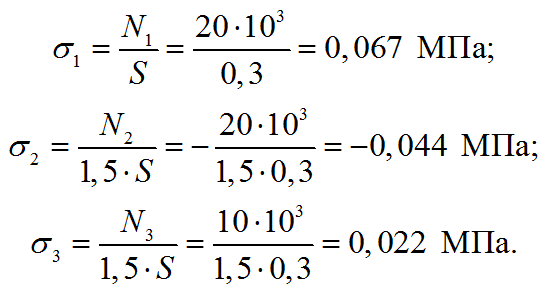
Строим эпюру нормальных напряжений (рисунок 1, г).
Максимальное нормальное напряжение возникает на первом участке: σ=0,067 МПа.
Определяем перемещение каждого участка стержня:

Определяем перемещение нижнего конца стержня:
![]()
Оставить свои комментарии и задать вопросы по задаче Вы можете в нашей группе «Вконтакте».

